Additive Phylogeny (no project to choose as WPB project)
This work-in-progress implementation is part of a contribution by Vanessa Leidel that aims to implement Additive Phylogeny from Bioinformatics algorithms (Compeau & Pevzner). The first half has already been solved, but the back-stepping procedure is still missing.
Introduction
Additive Phylogeny is a distance based approach to construct phylogenetic trees from an additive distance matrix. A distancematrix is the representation of nodes (species) and edges (distances between species) as a table and is additive, if you can recieve a unique simple unrooted tree fitting the distance matrix. Real world problems are mostly non additive, but parts of analyzing this problems are very similar to the additive phylogeny approaches (e.g. determining limb length). For this reason the implementation of the method additive Phylogeny is an important step in understanding computing evolutionary phylogenetic trees and solving special cases of real world problems
#r "nuget: FSharp.Stats, 0.5.0"
#r "nuget: FSharp.Data, 6.2.0"
open FSharp.Data
open FSharp.Stats
open System.Collections.Generic
creating a distance Matrix and proofing of Additivity
Before we start to implement the additive distance matrix approach, we create distance matrices and proof them on additivity. In this case the additive matrice needs to be symmetric and has indices representing the species (columnnumber / rownumber) and the values in the rows / columns representing the distance between two species. For example, if we start with the following matrix, than row j has indice one and the distance between j and i is 13. This matrices can be translated in coding language by creating a type DistanceMatrix, that has member species and DistanceM and a static member create to create the matrix.
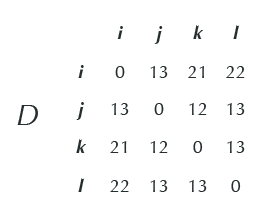
Fig.1. Example of a distance matrix at the beginn
// Dieser Typ soll die Distanzmatrix in Form eines Codes darstellen können, so dass auf die einzelnen Elemente zugegriffen werden kann.
// Species representiert dabei jeweils den Column/RowNamen und wird für die eigentliche Analyse nicht benötigt
// DistanceM representiert die eigentliche Distanzmatrix und ist vom Typ matrix
// Create ist notwendig um ein Element von diesem Typen zu erstellen
type DistanceMatrix<'a> = {
Species : string []
DistanceM : matrix
} with
static member Create species distanceM = {Species=species; DistanceM=distanceM}
create Example Matrices
In the following we create three different matrices to proof the functions for functionality.
This are myMatrixAdditive (a 44 matrice), twentyNineMatrix (2929 matrice) and non-additive matrice (4*4).
The first matrix was taken from chapter 7 of the book "Bioinformatics Algorithms: An Active Learning Approach", which describes the additive matrices approach and other phylogenetic methods.
The second matrix was taken as an example from the Rosalind page associated with the book.
The third matrix is self-made.
// Dieser Block kreiert eine 4*4 matrix, die aus dem Kapitel 7 des Buches "Bioinformatics Algorithms: An Active Learning Approach" entnommen wurde.
// Dabei wird ein 2D Array zunächst in eine Matrix umgewandelt sodass auf die Elemente durch z.B. myMatrixAdditive.DistanceM.[0,1] = 13 zugegriffen werden kann
// Anschließend wird die Distanzmatrix mit Rownamen verknüpft und erstellt
let myMatrixAdditive<'a> =
let distTest =
[|
[|0.;13.;21.;22.|]
[|13.;0.;12.;13.|]
[|21.;12.;0.;13.|]
[|22.;13.;13.;0.|]
|]
|> matrix
DistanceMatrix<'a>.Create [|"i";"j";"k";"l"|] distTest
// Hier wird eine 29*29 Matrix eingefügt.
// Dabei nutzt man eine externe Quelle und schneidet die Informationen dieser Quelle soweit zurecht, dass nur die notwendigen Informatinen behalten werden.
// Es handelt sich hierbei um die oben verlinkte Matrix
let twentyNineMatrix<'a> =
let test =
let rawData = Http.RequestString @"https://bioinformaticsalgorithms.com/data/extradatasets/evolution/Additive_Phylogeny.txt"
rawData.Split '\n'
|> Array.skip 2
|> Array.take 29
|> Array.map (fun x ->
x.Split ' '
|> Array.take 29
|> Array.map float
)
|> matrix
DistanceMatrix<'a>.Create [|"i";"j";"k";"l";"m";"n";"o";"p";"q";"r";"s";"t";"u";"v";"w";"x";"y";"z";"a";"b";"c";"d";"e";"f";"g";"h";"ii";"jj";"kk"|] test
// Hier wird eine non Additive Matrix, welche Symmetrie aufweist erstellt um die Funktion die auf Additivity überprüft zu prüfen auf Funktionalität
let myNonAdditiveAdditive<'a> =
let distTest =
[|
[|0.;3.;4.;3.|]
[|3.;0.;4.;5.|]
[|4.;4.;0.;2.|]
[|3.;5.;2.;0.|]
|]
|> matrix
DistanceMatrix<'a>.Create [|"i";"j";"k";"l"|] distTest
proofing of Additivity
One simple, less time consuming Way to proof a distanceMatrix for additivity is the four point condition . Looking if you can visit every node only once is very time intensive. For this reason the four point condition is the prefered method for big matrices (p.52). The four point condition explains that a matrix is additive, when the four point condition is true for every group of four indices of the matrix. The formula describing the condition is:
di,j + dk,l < = di,k + dj,l = di,l + dj,k
Furthermore we test if one indice is at least equal to the specCount, because this means that you call a species not present in the matrix.// Diese Formel nimmt eine matrix distMat sowie vier verschiedene speciesIndex als Input und berechnet entsprechend der Formel drei verschiedene Summen.
// Beispielsweise würde für myMatrix Additive sum 1 = 26 ; sum 2 = 34 (21+13) und sum 3 = 34 (22 + 12) true herauskommen.
let fourpoint_condition (distMat: matrix) (specIndex0:int) (specIndex1: int) (specIndex2: int) (specIndex3: int) =
let specCount = distMat.NumRows
if (specIndex0 >= specCount) || specIndex1 >=specCount ||specIndex2 >= specCount ||specIndex3 >= specCount then
failwithf "specIndex is not present in distance matrix"
let sum1 = distMat.[specIndex0,specIndex1] + distMat.[specIndex2,specIndex3]
let sum2 = distMat.[specIndex0,specIndex2] + distMat.[specIndex1,specIndex3]
let sum3 = distMat.[specIndex0,specIndex3] + distMat.[specIndex1,specIndex2]
(sum1 = sum2 && sum1 > sum3) || (sum1 = sum3 && sum1 > sum2) || sum2 = sum3 && sum2 > sum1
Because we have in Real World almost everywhere bigger Distancematrices, we need a dynamic version, that proofs for every possible group of four indices if it fullfills the four point condition and if not fail. To take care that you use every possible indice only one and not have twice the same species, we need one further test that reduces cumputation time.
// Diese Formel bestimmt zunächst die Anzahl der Reihen und Spalten und prüft ob diese gleich sind um die Symmetrie einer Matrix zu kontrollieren
// Anschließend wird in einer vierfach verschachtelten loop zunächst überprüft das der Specindex0 kleiner ist als alle anderen Species und Specindex 3 immer das größe ist
// Für jede dieser Kombinationen (z.B. in einer 29*29 Matrix: 1,2,3,4 ; 1,2,3,5; 1,2,3,6 .... 25,26,27,28) wird nun überprüft ob die Condition erfüllt ist und wenn nicht, wird sofort ein Error geworfen
let testingAdditivity (distMat: matrix) =
let rowlength = distMat.NumRows
let columnlength = distMat.NumCols
if rowlength <> columnlength then failwith " Matrix isnt symmetric, but has to be to have a phylogenetic tree"
for specIndex0 = 0 to (rowlength-1) do
for specIndex1 = 0 to (rowlength-1) do
for specIndex2 = 0 to (rowlength-1) do
for specIndex3 = 0 to (rowlength-1) do
if
specIndex0 < specIndex1
&& specIndex0 < specIndex2
&& specIndex0 < specIndex3
&& specIndex1 < specIndex2
&& specIndex1 < specIndex3
&& specIndex2 < specIndex3
then
if not (fourpoint_condition distMat specIndex0 specIndex1 specIndex2 specIndex3) then
failwithf "Matrix is non additive, but it has to be additive to fit a tree"
// test of testing additivity
testingAdditivity myMatrixAdditive.DistanceM
testingAdditivity twentyNineMatrix.DistanceM
testingAdditivity myNonAdditiveAdditive.DistanceM
|
The limb length problem
After we have tested if a Matrix is Additive, we need for the distance based approach some more formulas to construct the unique simple tree fitting the distance matrix. The appraoch that is described here in this documentation, is shown in the following picture. One of the key points to recieve the tree is to cumpute the limb length of an leaf y (y reprersents the index of the species node) to its parent node.
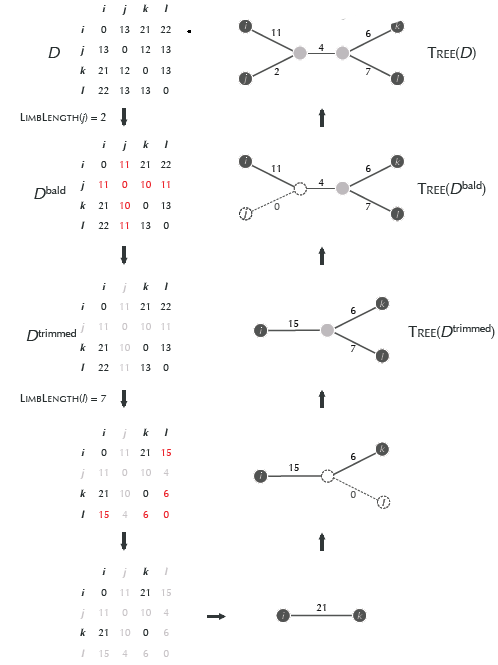
Fig.2. Converting the additive distance matrix into a simple tree fitting the matrix and steps
Figure 2 describes the procedure to get a tree fitting the distance Matrix. first you need to get the limbLength of a leaf y to its parent. A Leaf is always the present-day species. To get the minimal limbLength of an arbirtray leaf y (y can be every index present in the matrix) you have to determine every possible limbLength and take the minimal limblength. The formula to determine the limblength is therefore
Limblength(y) = (Di,y + Dy,k - Di,k)/2 , where y, i and k are three different species
Again we have to consider, that the specindex is present in the matrix and we introduce an error, when the specIndex is not present in the matrix// Diese Formel bekommt als Input die Distanzmatrix ohne Namen der Reihen / Spalten sowie drei verschiedene Indices, welche unterschiedliche Spezies repräsentieren.
// Dabei ist specIndex1 der Index der Species y (Species from Interest) und specIndex 2 und SpecIndex 3 die Species mit denen verglichen wird
// Zunächst wird geprüft ob alle Indices Teil der Matrix (< als die Größe), z.B. in einer 4*4 Matrix kleiner 4
// Wenn dies der Fall ist wird die Limblength für eine bestimmte Kombination berechnet, z.B. für Species j verglichen mit i und k --> (13+12-21/2) = 2
let LimblengthFormula (distMat:matrix) (specIndex1:int) (specIndex2:int) (specIndex3:int) =
let specCount = distMat.NumRows
if (specIndex1 >= specCount) || specIndex2 >=specCount || specIndex3 >= specCount then
failwithf "specIndex is not present in distance matrix"
(distMat.[specIndex2,specIndex1] + distMat.[specIndex1, specIndex3] - distMat.[specIndex2, specIndex3]) / 2.
As already described above, we need to get the minimal limblength of a distinct species y. For this reason we need to compute all possible limblength of the species y and comapre them with help of a for-loop, that computes for all combinations of species e.g. the limblength and store them in an Array. Again we consider that the specIndices are different and every combination has the species only once (e.g. 1 2 1 would lead to an error) and that we compute every combination only once (123 is the same as 132 and so you should only compute once). This can be reached by considering the symmetry of a distancematrix and taking specIndex 1 always as the smallest one.
// Hier wird für alle möglichen Kombinationen an Tripeln die Limblength einer bestimmten Spezies berechnet und in einem Array gespeichert.
// Anschließend soll die minimale Limblength bestimmt werden,dafür wird das kleinste Element des Arrays herasugefiltert
// Bsp. für myMatrixAdditive ist Limblength(l) = 7 , twentyNineMatrix hat limblength (Species28) = 890
let LimbLength (distMat: matrix) (specIndex: int) =
let specCount = distMat.NumRows
[|for specIndex2 = 0 to (specCount-1) do
for specIndex3 = 0 to (specCount-1) do
if (specIndex3 > specIndex2) && (specIndex3) <> (specIndex) && (specIndex) <> specIndex2 then
(LimblengthFormula (distMat) (specIndex) (specIndex2) (specIndex3))
|]
|>Array.min
// Test of LimblengthProblem
LimbLength myMatrixAdditive.DistanceM 3
LimbLength twentyNineMatrix.DistanceM 28
The Dbald Matrix
After we have succesful computed the limbLength we can prepare one further function. As shown in figure 2, the next step after finding the minimal limblength is constructing the Dbald Matrix. The Dbald Matrix is a matrix where you update your matrix by trimming the leaf (y) to a limblength = 0. This can be done by subtracting the distances shown in row / column y with the limbLength determined before. This Dbald matrix is needed to get informations about the length of edges between the species and where the attachmentpoint between a node y and another node is. To get the dbald Matrix of the corresponding distance Matrix we create first a function, that updates the values in the corresponding row / column.

Fig.3. Cumputing of the dBald Matrix
In this case you can recognize that column / row j is updated by reducing it with two eg. 13-2 = 11 for Di,j
// Diese Formel berechnet die Dbald Distanzen für jedes einzelne Feld.
// Dafür wird die Limblength der entsprechenden Spezies berechnet und die jeweilige Reihe / Spalte angegeben
// Der Aufruf updateDistancematrix (myMatrixAdditive.DistanceM) 1 0 1 führt z.B. zu 11 und entspricht dem Wert in Figur 3
let updateDistancematrix (distMat:matrix) (specIndexRow: int) (specIndexColumn: int) (specIndex: int) =
if distMat.[specIndexRow,specIndexColumn] = 0. then
0.
else
distMat.[specIndexRow,specIndexColumn] - LimbLength (distMat) (specIndex)
The updateDistanceMatrix function can now be used to update the complete row and column y. When all values are updated, than you get an new matrix Dbald shown in Figure 3 with red marked column / row. The changing in one function can simply be done using a 2 fold nested loop which contains an if clause that proofs if the values are equal to Rowindex and Columnindex and when not you need not to change the value.
// Hier wird die dBaldMatrix aus einer Distanzmatrix und gegebenen specIndex berechnet.
// Dafür wird eine verschachtelte loop benutzt, die zunächst in einem 2D Array alle Values speichert und dabei die entsprechende Reihe / Spalte ändert,
// wenn der Rowindex / Columnindex dem SpecIndex entspricht.
let dBaldMatrix (distMat:matrix) (specIndex: int) =
let specCountRow = distMat.NumRows
let specCountColumn = distMat.NumCols
[|for rowindex = 0 to specCountRow-1 do
[|for columnindex = 0 to specCountColumn-1 do
if rowindex = specIndex || columnindex = specIndex then
updateDistancematrix distMat rowindex columnindex specIndex
else
distMat.[rowindex,columnindex]
|]
|]
|> matrix
//Wendet man diese Formel z.B. für myMatrixAdditive.DistanceM 1 an so wird Spalte j und Reihe j verändert und es entsteht die Matrix aus Figur 2
//der Aufruf twentyNineMatrix.DistanceM 28 führt zur Veränderung der letzten Reihe -->
//8142.000 9688.000 4941.000 7419.000 5936.000 1736.000 9053.000 5337.000 1276.000 .... 0.000
// Test of Matrices
printfn "%A" (dBaldMatrix myMatrixAdditive.DistanceM 1)
printfn "%A" (dBaldMatrix twentyNineMatrix.DistanceM 28)
Trimming the Tree
When we look at Figure 2 we can recognize that next we need to come to the tree Dtrimmed. This Tree is different to Dbald, because we reduce the matrix and remove the changed columns. After we again construct Dbald and remove again column / row until we have a 2*2 matrix. The function to remove columns / rows can be found in the Fsharp.Stats library and is shown in the next Codeblock
//Hier wird die veränderte Reihe entfernt, da diese dem SpecIndex entspricht und die Matrix damit verringert
//Bsp. delete_species (dBaldMatrix (myMatrixAdditive.DistanceM) 1) führt zu
// 0 21 22
// 21 0 13
// 22 13 0
let delete_species (distMat:matrix) (specIndex: int) =
distMat
|> Matrix.removeColAt specIndex
|> Matrix.removeRowAt specIndex
Finding the Attachmentpoint of a leaf
Because we create the tree by Adding leaves backwards, we need a further function, we can prepare.
This function tries to identify the point of attachment of leaf y. To find the attachment point in the trimmed tree,
you should "consider that Tree Dbald, is the same as Tree (D), except that Limblength(j) = 0" (Compeau and Pevnzer, Bioinformatics Algorithms: An Active Learning Approach).
because we know from the Limblength theorom, that is integrated in dBald that leaves i and k muist be so that limblength(j)=0. This leads to the following assumption:
The attachmentpoint of a leaf j has to be located at distancei,jbald on a path connecting node i with node k in the trimmed tree.
When the attachmentpoint is at an existing node, we connect j to this node. otherwise if it occurs at an edge, we insert a new internal node at distance and connect j to it.
This explanation can now be translated in coding language.
//Hier wird der Attachmentpoint einer bestimmten leaf distinctLeaf bestimmt.
//Dafür wird eine dBaldMatrix bzw. trimmed matrix, sowie die leaf von Interesse als Input benötigt sowie die Anzahl der SpecIndices bestimmt
let attachmentPoint (dBald: matrix) (distinctLeaf: int) =
// entspricht der Anzahl an Specindices z.B. in einer 29 * 29 Matrix = 28
let NumberOfSpecies = dBald.NumRows-1
//in dieser verschachtelten For loop werden alle möglichen Attachmentpoints für eine bestimmte leaf bestimmt und in einem Array gespeichert
//z.B. für 29*29 matrix 0,26 = 8142 bis 26,27 = 868
[|for i = 0 to NumberOfSpecies-1 do
for j = i+1 to NumberOfSpecies-1 do
if dBald.[i,j] = (dBald.[i,distinctLeaf] + dBald.[distinctLeaf,j]) then
(i,j),dBald.[i,(distinctLeaf)]
|]
// Anschließend wird das Array in kleinere Arrays groupiert, wobei die Gruppierung nach gleicher Menge (i) erfolgt --> alle mit 0 in eine Gruppe usw.
|> Array.groupBy (fun ((i,j),d) -> i)
// Es wird das maximale Element herasugefiltert und dabei das erste Element desa Tupels genutzt, in diesem Fall z.B. 26
|> Array.maxBy fst
// nun wird auf alle Elemente dieser Gruppe zugegriffen und das erste Element behalten z.B hier (26,27), 868 -->
// diese sagt nun das auf der Strecke zwischen Knoten 26 und Knoten 27 auf der Distanz 868 ein weiterer Knoten liegen muss
|> snd
|> Array.head
// Test of Attachmentpoint
attachmentPoint (dBaldMatrix myMatrixAdditive.DistanceM 3) 3 // (1,2 -->6)
((attachmentPoint ( dBaldMatrix twentyNineMatrix.DistanceM 28)) 28) // (26,27--->868)
Creating a algorithm for distance-based phylogeny construction
After we have designed all essential functions for the additive phylogeny mechanism we can create an Algorithm for the finding of a simple tree fitting the n*n distance matrix D. For the creation of the Algorithm you can use either Figure 2 or the Pseudocode in Fig 5.

Fig.4 Pseudocode of Additive Phylogeny
But before we start to design the mechanism, we first create a type, where we can store the pathes and have a list which describes the created tree. This type is called PhylTreeConnection and contains the members SourceToTargetIndex and Distance. SourcetotargetIndex describes, which nodes are connected and distance how the distance is between the nodes. For example Fig.5. which shows a list how it should look like in the end
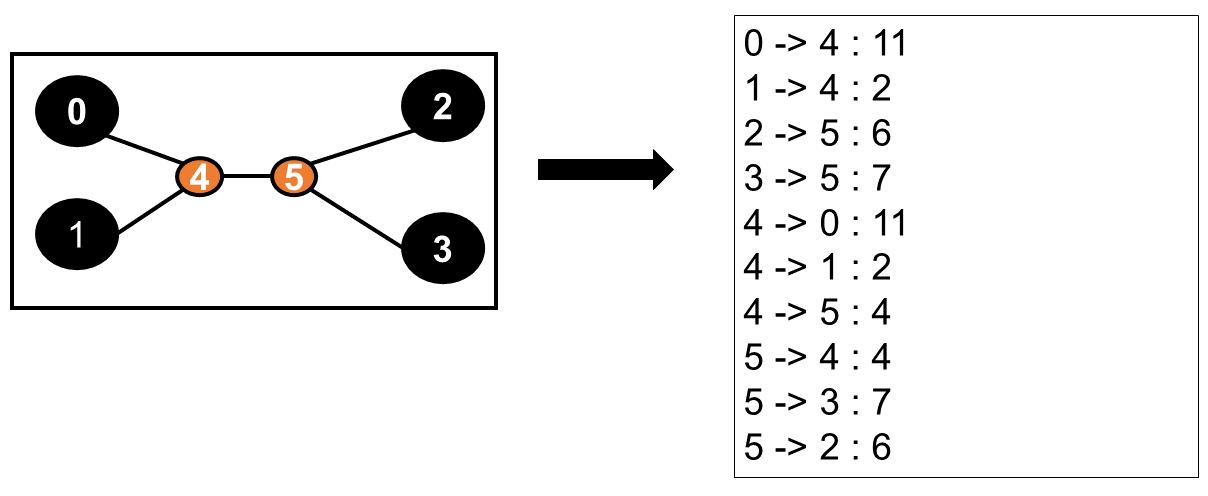
Fig.5. Example of a result
// Hier wird ein Typ deklariert, welche die Darstellung des phylogenetischen Baum am Ende ermöglicht
type PhylTreeConnection = {
SourceToTargetIndex: (int*int)
Distance: float
} with
static member Create sourceToTargetIndex distance = { SourceToTargetIndex= sourceToTargetIndex; Distance=distance}
Now we are able to create the phylogenetic tree with help of combinating the functions. The steps of the additive phylogeny Mechanism are described in the following steps:
- addPhyl is a function, which gets only the distancematrix as input and you proof first if the matrix is additive, because the function works only for additive matrices
-
Now we define some variables of the algorithm, that you need during the process:
- distmat is a mutable variable, that you need only as storage for the actual version of distanceMatrix,because you have to reduce this matrix until its a 2*2 Matrix
- n is again a mutable variable, that has to be always the last species (Row) of the Matrix and needs to be updated during algorithm
- lengthOfMatrix is a nonmutable variable, that stores the size of the input matrix
- resultList is a mutable variable, that is in the beginning empty and is needed as List to store the pathes at the end
- graph and attachmentsStore are two dictionaries, that stores all limbLength and distancematrices until we reach a length of 3*3 (graph) as well as the computed attachmentpoints for each matrixtype --> both habe the same length
- internalNodes is a mutable variable and describes the index of inserted nodes. It starts with the highest point and ends with the smallest
-
After we have defined all variables we can start with the algorithm, that in general consist of an if else clause. The if Part first proofs if we habe only a 2*2 matrix.
- If the size of distancematrix is 2*2, then the maximal Specindex n is 1 and we have directly the simple tree consisting of an single edge connecting both species and having size equal to the distance shown in the distancematrix
-
if we have no 2*2 Matrix then we have a quite more complex algorithm and we need the else part
- first we need to trimm the Matrix until its a 2*2 Matrix but store the updated matrix in each step. For each matrix (n), we also need to store the attachmentpoint as well. Here we use the defined dictionaries attachmentpoint and graph.
-
These dictionaries are filled in a simple while loop that has as termination condition size of matrix 2*2 (n < 2). The procedure of filling the dictionary is done in different steps
- First we fill for every round during loop graph by computing the corresponding limblength and the dBald matrix
- Then we can fill another dictionary that contains the attacghmentspoints as well as source and target
- Now we trimm the distancematrix in the same while loop and update n. The trimminmg is done be remove every time the last row / column in the matrix and n has always to be the specindex of the last row / column
-
After we have succesful reduced the the distancematrix iterative and stored the corresponding limblength and attachmentspoints in graph / attachmentsstore, we can start now with the Traceback, where the initial graph consisting of node 0 and 1 is updated by insering all corresponding nodes from attachmentsstore together with limblength stored in graph
For the Traceback we first update n, because we need n equal to 2 and we need to insert the single path of the 2*2 matrix being the starting point in resultlist, representing the tree. For this source is 0 , target is 1 and the distance is the distance represented in distancematrix.[0,1]. Because of symmetry source and target can also be changed and have the same distance. In this case target is 0 and source 1.
- Then we have to choose our first dBaldMatrix and the corresponding limblength and store this in a tuple (limblength,dMatix). For this we use n and assign the entry in graph to n
- In another tuple we store the first attachmentpoint as well as the corresponding src and target stored in attachmentsStore
- Next, we need to find the path in the actual tree that has to be modified. This path that has to be modified is assigned to edgeToModify. Attention: This Step is actually errorprone. Becuase we search after the first step in resultList for a path 1,2. But there exists no such Path. For this reason we need to find pathes were 1 is the src and we need to find a path were 2 is the target. This path are in this case (1,55) and (55,2). Then we must look at the distances from this pathes 2291 and 4032. Because the attachmentpoint between 1 and 2 is at 2678 we know that the attachmentpoint now has to be inserted on the path between 55,2 at distance size 387. This step is not working actually, becuase it actually searchs only after pathes being completely actual
- if we have found the path to modify in the resultList, we also need to assign the inverse path, because both pathes are part in the description of the simple tree. For that we only need to change the value of src in the value of target and target in src. The Distance is because of symmetry the same
-
Next we need to define, which pathes have to be added to the path. In general this are every time 2*3 different edges called A as well as their inverse path
- edgeAdditionA and edgeAdditionAinverse describe the Path from the src to internalNode and the length between them e.g. (0,55 with Distance 745)
- edgeAdditionB and edgeAdditionBinverse describe the path from the internal Node to the target and the Distance which is equal to the edgetomodify Distance - the computed Distance from attachmentpoint
- edgeAdditionC and edgeAdditionCinverse describe the Step where we add the next species (n) back to the tree (e.g.55 -2). This Path has the length limblength
- After Definition we update internalNodes and the resultList. While internalnodes has to be reduced by one, we have to remove the modified edges from resultList and add the computed edges, also n has to be increased by one
- To improve clarity we also have to sort the list by the Srcindex and then we can return the unique tree fitting the additive distancematrix
let addPhyl (distMat:matrix) =
//Hier wird getestet ob die in die Funktion gegebene distanzmatrix die Anforderungen einer additiven Matrix erfüllt,
//da der Algorithmus nur für eine additive Matrix funktionsfähig ist. Dafür wird die Funktion testingAdditivity aufgerufen.
testingAdditivity distMat
// Hier werden verschiedene Variablen (zum Teil veränderbar) deklariert. Diese werden im Laufe des Algorithmus benötigt und müssen zum Teil veränderbar sein
// veränderbare Variable, welche die aktuelle Version der Matrix beinhaltet, da die Matrix verändert werden muss (Stichwort Dbald)
let mutable dist_Mat = distMat
// veränderliche Varialble, die immer auf die letzte Reihe / Spalte der aktuellen Matrix verweist
let mutable n = dist_Mat.NumRows-1
// Unveränderliche Variable, welche auf die Länge der InputMatrix verweist
let lengthOfMatrix = distMat.NumRows-1
// Hier wird eine leere Liste vom Typ PhylTreeConnection deklariert in der die Pfade am Ende gelistet sind und der Tree beschrieben wird
let mutable resultList: PhylTreeConnection list = []
//Hier werden twei mutable dictionaries deklariert. graph ist dafür notwendig, alle Matrixen zu speichern und damit rückwärts auflösen zu können
//und enthält den Wert von n als Schlüssel ebensp wie der attachmentsstore der src,target und den attachmentPoint speichert.
let graph = new Dictionary<int,(float*matrix) >()
let attachmentsStore = new Dictionary<int,((int*int)*float)>()
// internalNodes ist die variable, welche den Index des einzufügenden Knoten deklariert
let mutable internalNodes = 2*dist_Mat.NumRows-3
// Hier wird geprüft, ob eine 2*2 Matrix vorliegt, oder eine größere Matrix.
// Wenn eine 2*2 Matrix vorliegt, dann muss der Algorithmus nicht weiter durchlaufen werden
// und es kann direkt der phylogenetische Baum, bestehend aus einer einfachen Verbindung der beiden Spezies erstellt werden.
// Die Länge der Verbindung entspricht der Distanz zwischen den beiden Spezies. Folglich wird der Baum in der Liste
// dargestellt durch den Eintrag von Source to Target (0,1) bzw. (1,0) und der Distanz zwischen beiden Spezies und die Liste wird zurückgegeben
if n = 1 then
let distance = dist_Mat.[0,1]
resultList <- {SourceToTargetIndex = (0,1); Distance = distance}::resultList
resultList <- {SourceToTargetIndex = (1,0); Distance = distance}::resultList
resultList
// Diese Verzweigung wird ausgeführt falls keine 2*2 Matrix vorliegt
else
// Hier werden die in Zeile 24 und 25 deklarieren Dictionaries graph und attachmentsStore solange gefüllt bis eine Matrixgröße 2+2 erreicht ist.
// Das Dictionary graph beinhaltet dabei als Schlüssel n und ordnet diesem die jeweilige limbLength sowie die Distanzmatrix zu aus welcher die aktuelle Pfad Länge entnommen werden kann
// Im Dictionary attachmentsStore werden die berechneten attachmentpoints von zwei Spezies gespeichert sowie src und target
while n >= 2 do
let limblength = LimbLength (dist_Mat) n
dist_Mat <- dBaldMatrix dist_Mat n
graph.Add (n,(limblength,dist_Mat))
// printfn "n: %i" n
// printfn "limblength: %f %A" limblength dist_Mat
// Beispielhafte Ausgabe wenn n = 3 erreicht ist, zur Ansicht was in dictionary graph gespeichert wird
// n: 3
// limblength: 409.000000
// 0 1 2 3
// 0 -> 0.000 3036.000 4777.000 1132.000
// 1 -> 3036.000 0.000 6323.000 2678.000
// 2 -> 4777.000 6323.000 0.000 3645.000
// 3 -> 1132.000 2678.000 3645.000 0.000
let attachment = attachmentPoint dist_Mat n
let x = snd attachment
let (src,target) = fst attachment
attachmentsStore.Add(n,((src,target),x))
// printfn " n: %i x: %f src: %i target:%i" n x src target
// Beispielshafte Ausgabe wenn n = 3 erreicht ist in der 29*29 Matrix aus Rosalind
// n: 3 x: 2678.000000 src: 1 target:2
// Hier wird die Matrix getrimmt und n geupdatet sodass n wieder dem Index der letzten Reihe / Spalte entspricht
dist_Mat <- delete_species dist_Mat n
n <- n-1
// Bis hier wurde die distanzmatrix iterativ reduziert und die jeweiligen Attachmentpoints und limblength in graph und attachmentsStore gespeichert
// Nun muss im TraceBack-Schritt in jeder Iteration ein initial graph bnestehen aus node 0 und 1 mit allen fehleden nodes vervollständigt werden. Diese werden
// an den punkten aus attachmentstore angefügt mit der limblength, die in graph gespeichert ist.
// Dafür wird zunächst der aktuelle Pfad der in der Matrix als Schnittpunkt 0,1 dargestellt ist in resultList eingefügt
resultList <- {SourceToTargetIndex = (0,1); Distance = distMat.[0,1]}::resultList
resultList <- {SourceToTargetIndex = (1,0); Distance = distMat.[1,0]}::resultList
// Hier wird n wieder angepasst sodass n = 2 ist und damit dem kleinsten Schlüssel in den Dictionaries entspricht
n <- n+1
// Im folgenden Schritt wird der traceback durchgeführt und nach und nach die bestimmten attachmentpoints eingefügt.
// Dafür wird eine zweite While loop erstellt die solange wie n nicht dem maximalen Specindex entspricht den Traceback durchführt.
let traceback =
while n < lengthOfMatrix do (
// Hier wird die aktuelle resultList für jeden Durchgang geprintet: printfn "resultList: %A" resultList, Bsp. zu Beginn und nach dem ersten Durchlauf
// resultList zu Beginn: [{ SourceToTargetIndex = (1, 0) Distance = 3036.0 }; { SourceToTargetIndex = (0, 1) Distance = 3036.0 }]
// resultList nach Durchgang 1:[{ SourceToTargetIndex = (0, 55) Distance = 745.0 }; { SourceToTargetIndex = (55, 0) Distance = 745.0 };
// { SourceToTargetIndex = (55, 1) Distance = 2291.0 };
// { SourceToTargetIndex = (1, 55) Distance = 2291.0 }; { SourceToTargetIndex = (55, 2) Distance = 4032.0 };
// { SourceToTargetIndex = (2, 55) Distance = 4032.0 }]
// Take the currentGraphElement
let (limblength,dMatrix) = graph.[n]
// Take the currentAttachmentPoint
let ((src,trg),distance) = attachmentsStore.[n]
// Hier kann Beispielshaft durch den Print Befehl überprüft werden; ob der Attachmentpoint richtig übertragen wurde - Ausgabe für twentyNineMatrix
// printfn "index: %i, src: %i, trg: %i, distance: %f"n src trg distance
// index: 2, src: 0, trg: 1, distance: 745.000000
// index: 3, src: 1, trg: 2, distance: 2678.000000
// Ab hier ist der Code noch nicht vollständig funcktionsfähig, da aktuell nur nach edgestomodify gesucht wird die genau dem src, target entsprechen, dies ist allerdings nicht ausreichend, da vorher bereits Pfade verändert wurden und im Pfad zwischen 1 und 2 z.B. schon eine internalNode eingefügt wurde
// Problem: Es soll nodeindex 3 auf dem path zwischen nodes 1 und 2 angefügt werden, aber dieser path ist nicht verfügbar weil im vorigsen schritt schon
// ein artificail node (55) zwischen 1 und 2 eingefügt wurde. Deswegen müsste man resultlist jetzt untersuchen nach dem Path 1 -> 2 und die edge identifizieren an der
// der zusätzliche node (54) angefügt werden soll (aufgrund der distanzen 1-55: 2291 und 55-2: 4032 müsste node 54 demnach zwischen 55 und 2 in der Distanz 387 eingesetzt werden
let edgeToModify =
resultList |> List.find (fun element ->
element.SourceToTargetIndex = (src,trg) ||
element.SourceToTargetIndex = (trg,src)
)
// Hier soll der inverse Path von edge to Modify (Bsp. von 0,1 => 1,0) bestimmt und zugeordnet werden, da dieser auch aus der Liste entnommen werden muss
let edgeToModifyInnverse = {SourceToTargetIndex = (snd (edgeToModify.SourceToTargetIndex),fst (edgeToModify.SourceToTargetIndex)); Distance = edgeToModify.Distance}
// Hier wird das im vorherigen Codeabschnitt bestimmte edgeToModify und der inverse Pfad bestimmt
// printfn " edgetomodify: %A , edgetomodify inverse: %A" edgeToModify edgeToModifyInnverse
// edgetomodify: { SourceToTargetIndex = (1, 0) Distance = 3036.0 } , edgetomodify inverse: { SourceToTargetIndex = (0, 1) Distance = 3036.0 }
// Hier werden die Pfade bestimmt, die in resultList hinzugefügt werden sollen und an welcher Stelle ein Knoten eingefügt werden soll
// edgeAdditionA: Beschreibt den Pfad zwischen der Quelle und dem einzufügnden internal Node (z.B. 0 -55 ==> Distance 745 oder 55-54 ==> distance 387 )
// edgeAdditionB: Beschreibt den Pfad zwischen InternalNodes und dem target also von z.B. 55-1 ==> 2291 oder 54 -2 ==> 1354.
// Dafür muss die edgeToModiy Distanz von den einzelnen Distanzen ( Distanzen der beteiligten Teilpfade / Attachmentpoindistanz) abgezogen werden.
// edgeAdditionC: Hier wird die aktuelle Spezies wieder zum Baum hinzugefügt im Abstand der limblength zum aktuellen InternalNode ( z.B. im ersten Schritt wird Spezies 2 wieder eingefüht)
let edgeAdditionA = {SourceToTargetIndex = (src,internalNodes); Distance = distance}
let edgeAdditionA_inverse = {SourceToTargetIndex = (internalNodes,src); Distance = distance}
let edgeAdditionB = {SourceToTargetIndex = (internalNodes,trg); Distance = edgeToModify.Distance - distance}
let edgeAdditionB_inverse = {SourceToTargetIndex = (trg, internalNodes); Distance = edgeToModify.Distance - distance}
let edgeAdditionC = {SourceToTargetIndex = (internalNodes,n); Distance = limblength}
let edgeAdditionC_inverse = {SourceToTargetIndex = (n,internalNodes); Distance = limblength}
// Beispielshafte Ausgabe nach dem ersten Durchlauf von edgeAddition A , edgeAddition B und edgeAddition C
// Edgeaddition A: { SourceToTargetIndex = (0, 55) Distance = 745.0 }
// edgeAdditionB: { SourceToTargetIndex = (55, 1) Distance = 2291.0 }
// edgeAdditionC: { SourceToTargetIndex = (55, 2) Distance = 4032.0 }
// Aktualisieren von internal Nodes
internalNodes <- internalNodes-1
// Hier wird der phylogenetische Baum geupdated.
// Dafür werden die zu verändernden Pfade zunächst aus der Liste entferent und anschließend werden die vorher bestimmten Pfade der Liste hinzugefügt.
// Zuletzt wird der übersichtlichkeithalber die Liste nach den Src sotiert und n geupdatet. Nach Beendigung der While Loop wird zuletzt die fertige resultList,
// welche den Baum beschreibt ausgegeben
let newResultList =
resultList
|> List.where (fun x -> x <> edgeToModify && x <> edgeToModifyInnverse)
|> List.append [edgeAdditionA;edgeAdditionA_inverse;edgeAdditionB;edgeAdditionB_inverse;edgeAdditionC;edgeAdditionC_inverse]
|>List.sortBy (fun x -> fst (x.SourceToTargetIndex))
resultList <- newResultList
n <- n+1
)
resultList
// Beispielshafte Ausgabe zur Darstellung des Problems
// printfn "resultList: %A" resultList
// printfn "index: %i, src: %i, trg: %i, distance: %f"n src trg distance
// resultList: [{ SourceToTargetIndex = (1, 0)
// Distance = 3036.0 }; { SourceToTargetIndex = (0, 1)
// Distance = 3036.0 }]
// index: 2, src: 0, trg: 1, distance: 745.000000
// resultList: [{ SourceToTargetIndex = (0, 55)
// Distance = 745.0 }; { SourceToTargetIndex = (55, 0)
// Distance = 745.0 }; { SourceToTargetIndex = (55, 1)
// Distance = 2291.0 };
// { SourceToTargetIndex = (1, 55)
// Distance = 2291.0 }; { SourceToTargetIndex = (55, 2)
// Distance = 4032.0 }; { SourceToTargetIndex = (2, 55)
// Distance = 4032.0 }]
// index: 3, src: 1, trg: 2, distance: 2678.000000
// test off addPhyl
addPhyl twentyNineMatrix.DistanceM
|
namespace FSharp
--------------------
namespace Microsoft.FSharp
namespace FSharp.Data
--------------------
namespace Microsoft.FSharp.Data
val string : value:'T -> string
<summary>Converts the argument to a string using <c>ToString</c>.</summary>
<remarks>For standard integer and floating point values the and any type that implements <c>IFormattable</c><c>ToString</c> conversion uses <c>CultureInfo.InvariantCulture</c>. </remarks>
<param name="value">The input value.</param>
<returns>The converted string.</returns>
--------------------
type string = System.String
<summary>An abbreviation for the CLI type <see cref="T:System.String" />.</summary>
<category>Basic Types</category>
val matrix : ll:seq<#seq<float>> -> Matrix<float>
--------------------
type matrix = Matrix<float>
<summary> Utilities for working with network via HTTP. Includes methods for downloading resources with specified headers, query parameters and HTTP body </summary>
System.String.Split(separator: string [], options: System.StringSplitOptions) : string []
System.String.Split(separator: string,?options: System.StringSplitOptions) : string []
System.String.Split(separator: char [], options: System.StringSplitOptions) : string []
System.String.Split(separator: char [], count: int) : string []
System.String.Split(separator: char,?options: System.StringSplitOptions) : string []
System.String.Split(separator: string [], count: int, options: System.StringSplitOptions) : string []
System.String.Split(separator: string, count: int,?options: System.StringSplitOptions) : string []
System.String.Split(separator: char [], count: int, options: System.StringSplitOptions) : string []
System.String.Split(separator: char, count: int,?options: System.StringSplitOptions) : string []
module Array from FSharp.Stats
<summary> Module to compute common statistical measure on array </summary>
--------------------
module Array from Microsoft.FSharp.Collections
<summary>Contains operations for working with arrays.</summary>
<remarks> See also <a href="https://docs.microsoft.com/dotnet/fsharp/language-reference/arrays">F# Language Guide - Arrays</a>. </remarks>
--------------------
type Array = new : unit -> Array static member geomspace : start:float * stop:float * num:int * ?IncludeEndpoint:bool -> float array static member linspace : start:float * stop:float * num:int * ?IncludeEndpoint:bool -> float []
--------------------
new : unit -> Array
<summary>Builds a new array that contains the elements of the given array, excluding the first N elements.</summary>
<param name="count">The number of elements to skip.</param>
<param name="array">The input array.</param>
<returns>A copy of the input array, after removing the first N elements.</returns>
<exception cref="T:System.ArgumentNullException">Thrown when the input array is null.</exception>
<exception cref="T:System.ArgumentExcepion">Thrown when count is negative or exceeds the number of elements in the array.</exception>
<summary>Returns the first N elements of the array.</summary>
<remarks>Throws <c>InvalidOperationException</c> if the count exceeds the number of elements in the array. <c>Array.truncate</c> returns as many items as the array contains instead of throwing an exception.</remarks>
<param name="count">The number of items to take.</param>
<param name="array">The input array.</param>
<returns>The result array.</returns>
<exception cref="T:System.ArgumentNullException">Thrown when the input array is null.</exception>
<exception cref="T:System.ArgumentException">Thrown when the input array is empty.</exception>
<exception cref="T:System.InvalidOperationException">Thrown when count exceeds the number of elements in the list.</exception>
<summary>Builds a new array whose elements are the results of applying the given function to each of the elements of the array.</summary>
<param name="mapping">The function to transform elements of the array.</param>
<param name="array">The input array.</param>
<returns>The array of transformed elements.</returns>
<exception cref="T:System.ArgumentNullException">Thrown when the input array is null.</exception>
val float : value:'T -> float (requires member op_Explicit)
<summary>Converts the argument to 64-bit float. This is a direct conversion for all primitive numeric types. For strings, the input is converted using <c>Double.Parse()</c> with InvariantCulture settings. Otherwise the operation requires an appropriate static conversion method on the input type.</summary>
<param name="value">The input value.</param>
<returns>The converted float</returns>
--------------------
[<Struct>] type float = System.Double
<summary>An abbreviation for the CLI type <see cref="T:System.Double" />.</summary>
<category>Basic Types</category>
--------------------
type float<'Measure> = float
<summary>The type of double-precision floating point numbers, annotated with a unit of measure. The unit of measure is erased in compiled code and when values of this type are analyzed using reflection. The type is representationally equivalent to <see cref="T:System.Double" />.</summary>
<category index="6">Basic Types with Units of Measure</category>
val int : value:'T -> int (requires member op_Explicit)
<summary>Converts the argument to signed 32-bit integer. This is a direct conversion for all primitive numeric types. For strings, the input is converted using <c>Int32.Parse()</c> with InvariantCulture settings. Otherwise the operation requires an appropriate static conversion method on the input type.</summary>
<param name="value">The input value.</param>
<returns>The converted int</returns>
--------------------
[<Struct>] type int = int32
<summary>An abbreviation for the CLI type <see cref="T:System.Int32" />.</summary>
<category>Basic Types</category>
--------------------
type int<'Measure> = int
<summary>The type of 32-bit signed integer numbers, annotated with a unit of measure. The unit of measure is erased in compiled code and when values of this type are analyzed using reflection. The type is representationally equivalent to <see cref="T:System.Int32" />.</summary>
<category>Basic Types with Units of Measure</category>
<summary>Print to a string buffer and raise an exception with the given result. Helper printers must return strings.</summary>
<param name="format">The formatter.</param>
<returns>The formatted result.</returns>
<summary>Throw a <see cref="T:System.Exception" /> exception.</summary>
<param name="message">The exception message.</param>
<returns>The result value.</returns>
<summary>Negate a logical value. Not True equals False and not False equals True</summary>
<param name="value">The value to negate.</param>
<returns>The result of the negation.</returns>
<summary>Returns the lowest of all elements of the array, compared via Operators.min.</summary>
<remarks>Throws ArgumentException for empty arrays</remarks>
<param name="array">The input array.</param>
<exception cref="T:System.ArgumentNullException">Thrown when the input array is null.</exception>
<exception cref="T:System.ArgumentException">Thrown when the input array is empty.</exception>
<returns>The minimum element.</returns>
<summary>Print to <c>stdout</c> using the given format, and add a newline.</summary>
<param name="format">The formatter.</param>
<returns>The formatted result.</returns>
module Matrix from FSharp.Stats
--------------------
type Matrix<'T> = | DenseRepr of DenseMatrix<'T> | SparseRepr of SparseMatrix<'T> interface IMatrixFormattable interface IFsiFormattable interface IEnumerable interface IEnumerable<'T> interface IStructuralEquatable interface IStructuralComparable interface IComparable override Equals : yobj:obj -> bool member Format : rowStartCount:int * rowEndCount:int * columnStartCount:int * columnEndCount:int * showInfo:bool -> string + 2 overloads member FormatStrings : rowStartCount:int * rowEndCount:int * columnStartCount:int * columnEndCount:int -> string [] [] ...
<summary> Removes a column at a given index </summary>
<summary> Removes a row at a given index </summary>
<summary>Applies a key-generating function to each element of an array and yields an array of unique keys. Each unique key contains an array of all elements that match to this key.</summary>
<param name="projection">A function that transforms an element of the array into a comparable key.</param>
<param name="array">The input array.</param>
<returns>The result array.</returns>
<exception cref="T:System.ArgumentNullException">Thrown when the input array is null.</exception>
<summary>Returns the greatest of all elements of the array, compared via Operators.max on the function result.</summary>
<remarks>Throws ArgumentException for empty arrays.</remarks>
<param name="projection">The function to transform the elements into a type supporting comparison.</param>
<param name="array">The input array.</param>
<exception cref="T:System.ArgumentNullException">Thrown when the input array is null.</exception>
<exception cref="T:System.ArgumentException">Thrown when the input array is empty.</exception>
<returns>The maximum element.</returns>
<summary>Return the first element of a tuple, <c>fst (a,b) = a</c>.</summary>
<param name="tuple">The input tuple.</param>
<returns>The first value.</returns>
<summary>Return the second element of a tuple, <c>snd (a,b) = b</c>.</summary>
<param name="tuple">The input tuple.</param>
<returns>The second value.</returns>
<summary>Returns the first element of the array.</summary>
<param name="array">The input array.</param>
<returns>The first element of the array.</returns>
<exception cref="T:System.ArgumentNullException">Thrown when the input array is null.</exception>
<exception cref="T:System.ArgumentException">Thrown when the input array is empty.</exception>
<summary>The type of immutable singly-linked lists. </summary>
<remarks>See the <see cref="T:Microsoft.FSharp.Collections.ListModule" /> module for further operations related to lists. Use the constructors <c>[]</c> and <c>::</c> (infix) to create values of this type, or the notation <c>[1; 2; 3]</c>. Use the values in the <c>List</c> module to manipulate values of this type, or pattern match against the values directly. See also <a href="https://docs.microsoft.com/dotnet/fsharp/language-reference/lists">F# Language Guide - Lists</a>. </remarks>
type Dictionary<'TKey,'TValue> = interface ICollection<KeyValuePair<'TKey,'TValue>> interface IEnumerable<KeyValuePair<'TKey,'TValue>> interface IEnumerable interface IDictionary<'TKey,'TValue> interface IReadOnlyCollection<KeyValuePair<'TKey,'TValue>> interface IReadOnlyDictionary<'TKey,'TValue> interface ICollection interface IDictionary interface IDeserializationCallback interface ISerializable ...
<summary>Represents a collection of keys and values.</summary>
<typeparam name="TKey">The type of the keys in the dictionary.</typeparam>
<typeparam name="TValue">The type of the values in the dictionary.</typeparam>
--------------------
Dictionary() : Dictionary<'TKey,'TValue>
Dictionary(dictionary: IDictionary<'TKey,'TValue>) : Dictionary<'TKey,'TValue>
Dictionary(collection: IEnumerable<KeyValuePair<'TKey,'TValue>>) : Dictionary<'TKey,'TValue>
Dictionary(comparer: IEqualityComparer<'TKey>) : Dictionary<'TKey,'TValue>
Dictionary(capacity: int) : Dictionary<'TKey,'TValue>
Dictionary(dictionary: IDictionary<'TKey,'TValue>, comparer: IEqualityComparer<'TKey>) : Dictionary<'TKey,'TValue>
Dictionary(collection: IEnumerable<KeyValuePair<'TKey,'TValue>>, comparer: IEqualityComparer<'TKey>) : Dictionary<'TKey,'TValue>
Dictionary(capacity: int, comparer: IEqualityComparer<'TKey>) : Dictionary<'TKey,'TValue>
type List = new : unit -> List static member geomspace : start:float * stop:float * num:int * ?IncludeEndpoint:bool -> float list static member linspace : start:float * stop:float * num:int * ?IncludeEndpoint:bool -> float list
--------------------
type List<'T> = interface ICollection<'T> interface IEnumerable<'T> interface IEnumerable interface IList<'T> interface IReadOnlyCollection<'T> interface IReadOnlyList<'T> interface ICollection interface IList new : unit -> unit + 2 overloads member Add : item: 'T -> unit ...
<summary>Represents a strongly typed list of objects that can be accessed by index. Provides methods to search, sort, and manipulate lists.</summary>
<typeparam name="T">The type of elements in the list.</typeparam>
--------------------
new : unit -> List
--------------------
List() : List<'T>
List(collection: IEnumerable<'T>) : List<'T>
List(capacity: int) : List<'T>
<summary>Returns the first element for which the given function returns True. Raises <c>KeyNotFoundException</c> if no such element exists.</summary>
<param name="predicate">The function to test the input elements.</param>
<param name="list">The input list.</param>
<exception cref="T:System.Collections.Generic.KeyNotFoundException">Thrown if the predicate evaluates to false for all the elements of the list.</exception>
<returns>The first element that satisfies the predicate.</returns>
<summary>Returns a new list containing only the elements of the list for which the given predicate returns "true"</summary>
<param name="predicate">The function to test the input elements.</param>
<param name="list">The input list.</param>
<returns>A list containing only the elements that satisfy the predicate.</returns>
<summary>Returns a new list that contains the elements of the first list followed by elements of the second.</summary>
<param name="list1">The first input list.</param>
<param name="list2">The second input list.</param>
<returns>The resulting list.</returns>
<summary>Sorts the given list using keys given by the given projection. Keys are compared using <see cref="M:Microsoft.FSharp.Core.Operators.compare" />.</summary>
<remarks>This is a stable sort, i.e. the original order of equal elements is preserved.</remarks>
<param name="projection">The function to transform the list elements into the type to be compared.</param>
<param name="list">The input list.</param>
<returns>The sorted list.</returns>