NB04b Peptide Identification

Download Notebook

1. Understanding peptide identification from MS2 spectra
2. Matching and scoring of Tandem MS peptide identification
   1. Step 1: Data acquisition and preprocessing
   2. Step 2: Preselecting the peptides of interest
   3. Step 3+4: Matching and Scoring

Understanding peptide identification from MS2 spectra

Under low-energy fragmentation conditions, peptide fragment patterns are reproducible and, in general, predictable, which allows for an amino acid sequence identification according to a fragmentation expectation. Algorithms for peptide identification perform in principle three basic tasks:

(i) a raw data preprocessing step is applied to the MS/MS spectra to obtain clean peak information. The same signal filtering and background subtraction methods are used as discussed in the section of low-level processing. Peak detection, however, may be performed differently. Preprocessing of MS/MS spectra focuses on the extraction of the precise m/z of the peak rather than the accurate peak areas. The conversion of a peak profile into the corresponding m/z and intensity values reduces the complexity, its representation is termed centroiding. To extract the masses for identification in a simple and fast way, peak fitting approaches are used. These approaches take either the most intense point of the peak profile, fit a Lorentzian distribution to the profile, or use a quadratic fit.

(ii) Spectrum information and possible amino acid sequences assignments are evaluated.

(iii) The quality of the match between spectrum and possible sequences is scored.

Even though the three steps roughly describe the basic principle of algorithms used for peptide sequence identification, most implementations show differences in individual steps which can lead to major changes in the outcome. Therefore, it has been proven useful to utilize more than one algorithm for a robust and thorough identification. Due to their major difference in identification strategies and prerequisites, identification algorithms are normally classified into three categories: (i) de novo peptide sequencing, (ii) peptide sequence-tag (PST) searching, and (iii) uninterpreted sequence searching. However, in this notebook we focus on the explanation of (iii) uninterpreted sequence searching, the most frequently used methods.

Matching and scoring of Tandem MS peptide identification

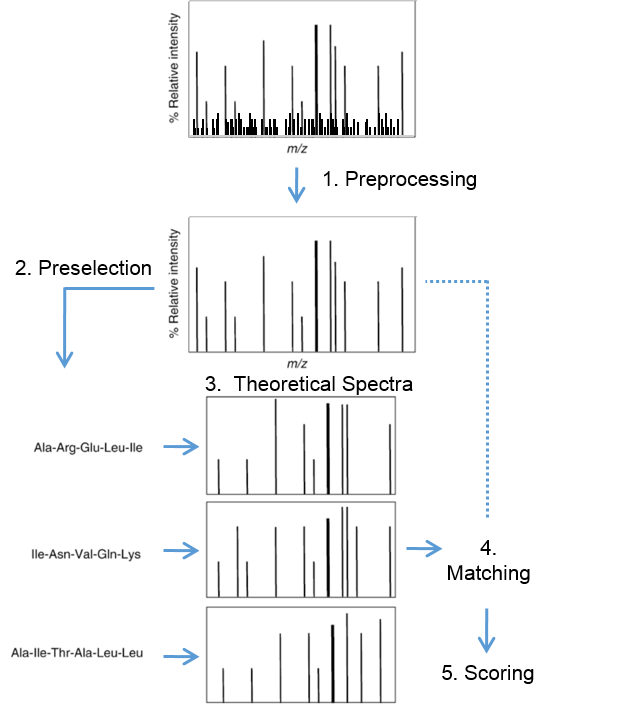
Figure 6: Process of computational identification of peptides from their fragment spectra

Previously we learned, that peptides fragment to create patterns characteristic of a specific amino acid sequence. These patterns are reproducible and, in general, predictable taking the applied fragmentation method into account. This can be used for computational identification of peptides from their fragment spectra. This process can be subdivided into 5 main steps: spectrum preprocessing, selection of possible sequences, generating theoretical spectra, matching and scoring (Figure 6). The first step is a preprocessing of the experimental spectra and is done to reduce noise. Secondly, all possible amino acid sequences are selected which match the particular precursor peptide mass. The possible peptides can but do not need to be restricted to a particular organism. A theoretical spectrum is predicted for each of these amino acid sequences. Matching and scoring is performed by comparing experimental spectra to their predicted corresponding theoretical spectra. The score function measures the closeness of fit between the experimental acquired and theoretical spectrum. There are many different score functions, which can be considered as the main reason of different identifications considering different identification algorithm. The most natural score function is the cross correlation score (xcorr) used by the commercially available search tool SEQUEST. One of the reasons the xcorr is so sensitive is because it involves a correction factor that assesses the background correlation for each acquired spectrum and the theoretically predicted spectrum from sequences within a database. To compute this correction factor, a measure of similarity is calculated at different offsets between a preprocessed mass spectrum and a theoretical spectrum. The final xcorr is then the correlation at zero offset minus the mean correlation from all the individual offsets.

Thus, the correlation function measures the coherence of two signals by, in effect, translating one signal across the other. This can be mathematically achieved using the formula for cross-correlation in the form for discrete input signals:

Equation 5

where x(i) is a peak of the reconstructed spectrum at position i and y(i) is a peak of the experimental spectrum. The displacement value 𝜏 is the amount by which the signal is offset during the translation and is varied over a range of values. If two signals are the same, the correlation function should have its maxima at 𝜏=0, where there is no offset. The average of the offset-correlation is seen as the average background correlation and needs to be subtracted from the correlation at 𝜏=0. It follows:

Equation 6

In practice many theoretical spectra have to be matched again a single experimental spectrum. Therefore, the calculation can be speed up by reformulating Equation 5 and Equation 6 and introduce a preprocessing step, which is independent of the predicted spectra.

Equation 7

For the preprocessed experimental spectrum y' it follows:

Equation 8

where:

Equation 9

Matching a measured spectrum against chlamy database

#r "nuget: BioFSharp, 2.0.0-beta4"
#r "nuget: BioFSharp.IO, 2.0.0-beta4"
#r "nuget: Plotly.NET, 4.2.0"
#r "nuget: BioFSharp.Mz, 0.1.5-beta"
#r "nuget: BIO-BTE-06-L-7_Aux, 0.0.10"

#if IPYNB
#r "nuget: Plotly.NET.Interactive, 4.2.0"
#endif // IPYNB

open Plotly.NET
open BioFSharp
open BioFSharp.Mz
open BIO_BTE_06_L_7_Aux.FS3_Aux
open System.IO

Step 1: Data acquisition and preprocessing

We load a single MS2 spectrum that is saved in a mgf file.

// Code-Block 1
let directory = __SOURCE_DIRECTORY__
let path = Path.Combine[|directory;"downloads/ms2sample.mgf"|]
downloadFile path "ms2sample.mgf" "bio-bte-06-l-7"

let ms2 = 
    BioFSharp.IO.Mgf.readMgf path
    |> List.head
    
ms2

No value returned by any evaluator

Here, the spectrum is already centroidized as shown in NB03c_Centroidisation.ipynb using the function msPeakPicking. So we just visualize mass and intensity:

// Code-Block 2

let ms2Chart = 
    Chart.Column(ms2.Intensity, ms2.Mass) 
    |> Chart.withTemplate ChartTemplates.light


ms2Chart

No value returned by any evaluator

Now, we will preprocess the experimental spectrum from our example. This is on the one hand to reduce noise, but also to make the measured spectrum more like the once we are able to simulate.

// Code-Block 3

let lowerScanLimit = 150.
let upperScanLimit = 1000.

let preprocessedIntesities =
    Mz.PeakArray.zip ms2.Mass ms2.Intensity
    |> (fun pa -> Mz.PeakArray.peaksToNearestUnitDaltonBinVector pa lowerScanLimit upperScanLimit)
    |> (fun pa -> Mz.SequestLike.windowNormalizeIntensities pa 10)
    
let intensityChart = 
    Chart.Column(preprocessedIntesities, [lowerScanLimit .. upperScanLimit])
    |> Chart.withTemplate ChartTemplates.light

intensityChart

No value returned by any evaluator

Step 2: Preselecting the peptides of interest

Every MS2 spectrum is accompanied by a m/z ratio reported by the instrument. Additionally, we can estimate the charge looking at the isotopic cluster. We take the peptide "DTDILAAFR" from our previous notebook again. Our example has a measured m/z = 511.2691141 and a charge of z=2.

let peptideMass = 
    Mass.ofMZ 511.2691141 2.

peptideMass

No value returned by any evaluator

From our previos notebook NB02b_Digestion_and_mass_calculation.ipynb, we know how to calculate all peptide masses that we can expect to be present in Chlamydomonas reinhardtii.

// Code-Block 4
let path2 = Path.Combine[|directory;"downloads/Chlamy_JGI5_5(Cp_Mp).fasta"|]
downloadFile path2 "Chlamy_JGI5_5(Cp_Mp).fasta" "bio-bte-06-l-7"

let peptideAndMasses = 
    path2
    |> IO.FastA.fromFile BioArray.ofAminoAcidString
    |> Seq.toArray
    |> Array.mapi (fun i fastAItem ->
        Digestion.BioArray.digest Digestion.Table.Trypsin i fastAItem.Sequence
        |> Digestion.BioArray.concernMissCleavages 0 0
    )
    |> Array.concat
    |> Array.map (fun peptide ->
        // calculate mass for each peptide
        peptide.PepSequence, BioSeq.toMonoisotopicMassWith (BioItem.monoisoMass ModificationInfo.Table.H2O) peptide.PepSequence
    )

peptideAndMasses |> Array.head

No value returned by any evaluator

However, we are only interest in possible amino acid sequences, that match the particular precursor peptide mass of our example spectrum with 1020.523675 Da. Additionaly, we should also consider a small measurement error.

// Code-Block 5

peptideAndMasses
|> Array.filter (fun (sequence,mass) -> mass > 1020.52  && mass < 1020.53)

No value returned by any evaluator

In the previous notebook NB04a_Fragmentation_for_peptide_identification.ipynb, we used functions that generate the theoretical series of b- and y-ions from the given peptide. Combined with the function Mz.SequestLike.predictOf that generates theoretical spectra that fit the Sequest scoring algorithm.

// Code-Block 6

let predictFromSequence peptide =
    [
        peptide
        |> Mz.Fragmentation.Series. yOfBioList BioItem.initMonoisoMassWithMemP
        peptide
        |> Mz.Fragmentation.Series.bOfBioList BioItem.initMonoisoMassWithMemP
    ]
    |> List.concat
    |> Mz.SequestLike.predictOf (lowerScanLimit,upperScanLimit) 2.

Step 3+4: Matching and Scoring

In the matching step, we compare theoretical spectra of peptides within our precursor peptide mass range with our measured spectra. We get a score which tells us how well the theoretical spectrum fits the given experimental spectrum.

// Code-Block 7
let sortedScores = 
    peptideAndMasses
    |> Array.filter (fun (sequence,mass) ->
        mass > 1020.52  && mass < 1020.53
    )
    |> Array.map (fun (sequence,mass)    ->
        sequence,predictFromSequence sequence
    )
    |> Array.map (fun (sequence,theoSpectrum) -> 
        sequence,BioFSharp.Mz.SequestLike.scoreSingle theoSpectrum preprocessedIntesities
    )
    |> Array.sortByDescending (fun (sequence,score) -> score)

sortedScores 

No value returned by any evaluator

Finally, we pick the sequence with the best score and are done for now. Notice however, that in a real world we would need to relate our score to the complete data set to get an idea of the overall quality and which numerical value we could trust.

Questions

1. How does the Chart change, when you change the value of 'numberofwindows' from 10 to 20? What does this parameter specify? (Code-Block 3)
2. What is the rational behind the normalization of measured spectra?
3. Why are we adding the mass of water to the peptide sequence? (BioItem.monoisoMass ModificationInfo.Table.H2O) (Code-Block 4)
4. In code block 6 you get a raw estimate on how many peptide sequences are candidates for a match, when given a certain mz. Given that one MS run can consist of up to 120.000 ms2 spectra, how many peptide spectrum matches do you have to perform? What does that mean for the performance of the application? Which parameters influence the size of the "search space"? (Code-Block 6)
5. What happens when you choose different lower and upper scan limits?
6. Visualize the distribution of scores using a histogram. (Code-Block 7)